直方图均衡(Histogram Equalization)
1. 灰度变换前后直方图的关系
-
灰度变换
DB=f(DA)
-
灰度变换后灰度直方图的关系

对于某一灰度值,其直方图数值和灰度变化后对于的灰度值的直方图数值相同
∫DBDB+ΔDBHB(DB)dD=∫DADA+ΔDAHA(DA)dD
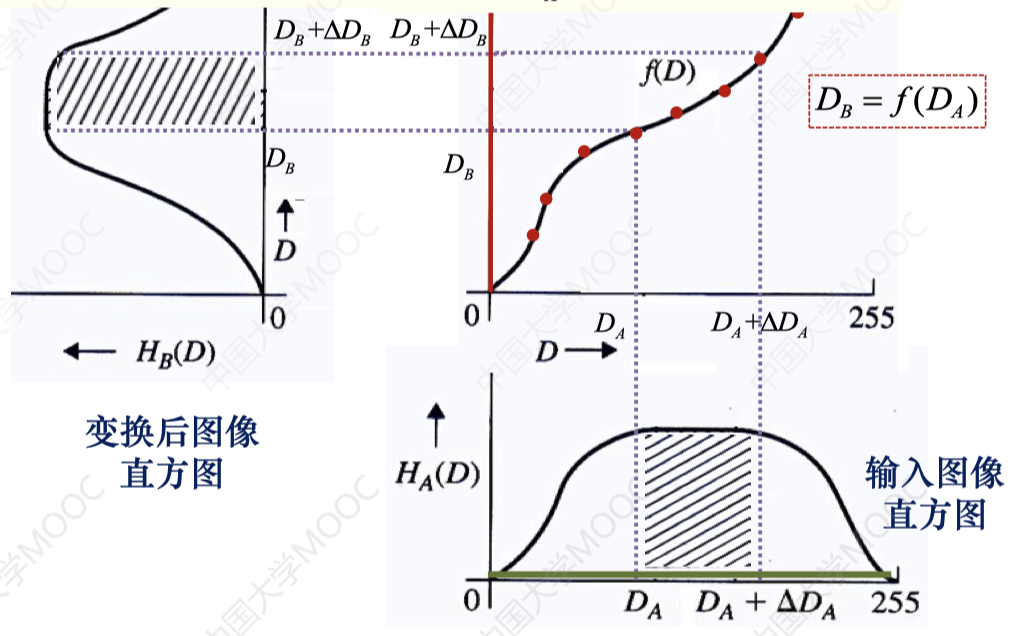
∫DBDB+ΔDBHB(DB)dD=∫DADA+ΔDAHA(DA)dD
HB(D)ΔDB=HA(D)ΔDA
HB(DB)=ΔDB/ΔDAHA(DA)
当ΔDA→0,ΔDB→0,
HB(DB)=dDB/dDAHA(DA)
代入DB=f(DA),
dDB/dDA=df(DA)/dDA
HB(DB)=f′(DA)HA(DA)
因此,灰度变换后图像直方图是变换前直方图与变换函数导数之比。
-
例子

2. 直方图均衡
直方图均衡的作用:
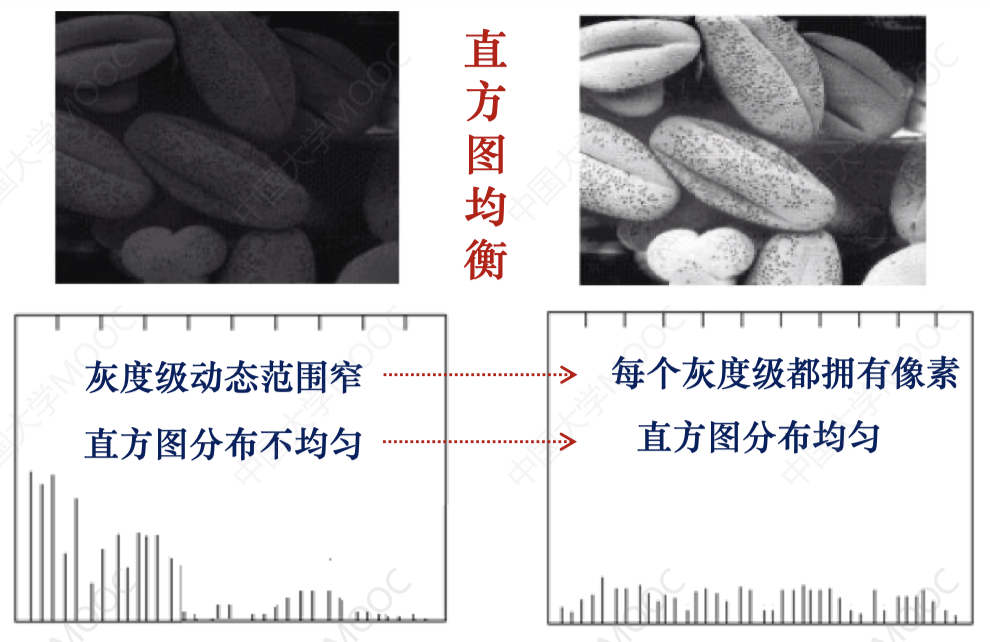
那能实现直方图均衡的灰度变换是什么?

直方图均衡后,每个灰度级拥有相同的像素个数:
HB(DB)=常数
HB(DB)=f′(DA)HA(DA)=常数=DmA0
其中Dm 代表灰度级(最大可能像素值的大小), A0 代表图像像素总数。
f′(DA)=A0Dm⋅HA(DA)
对两边同时积分,
f(DA)=A0Dm⋅0∑DAHA(DA)
DB=A0Dm⋅0∑DAHA(DA)
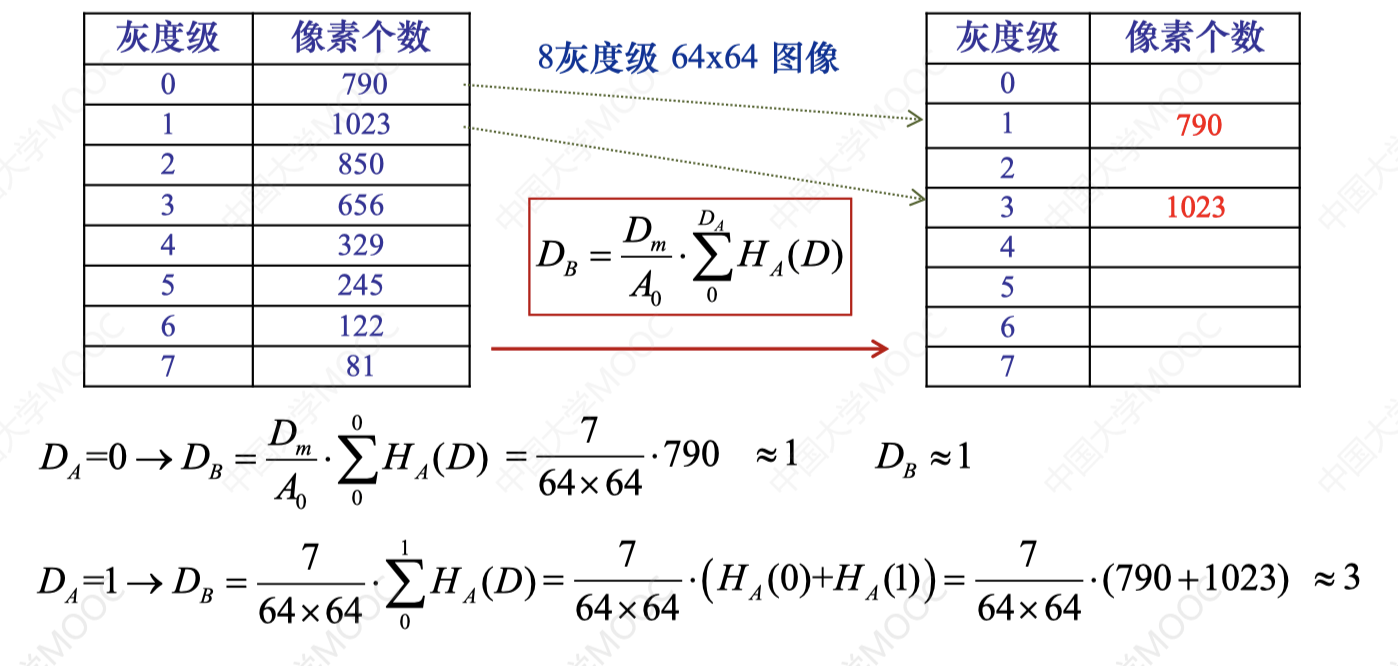
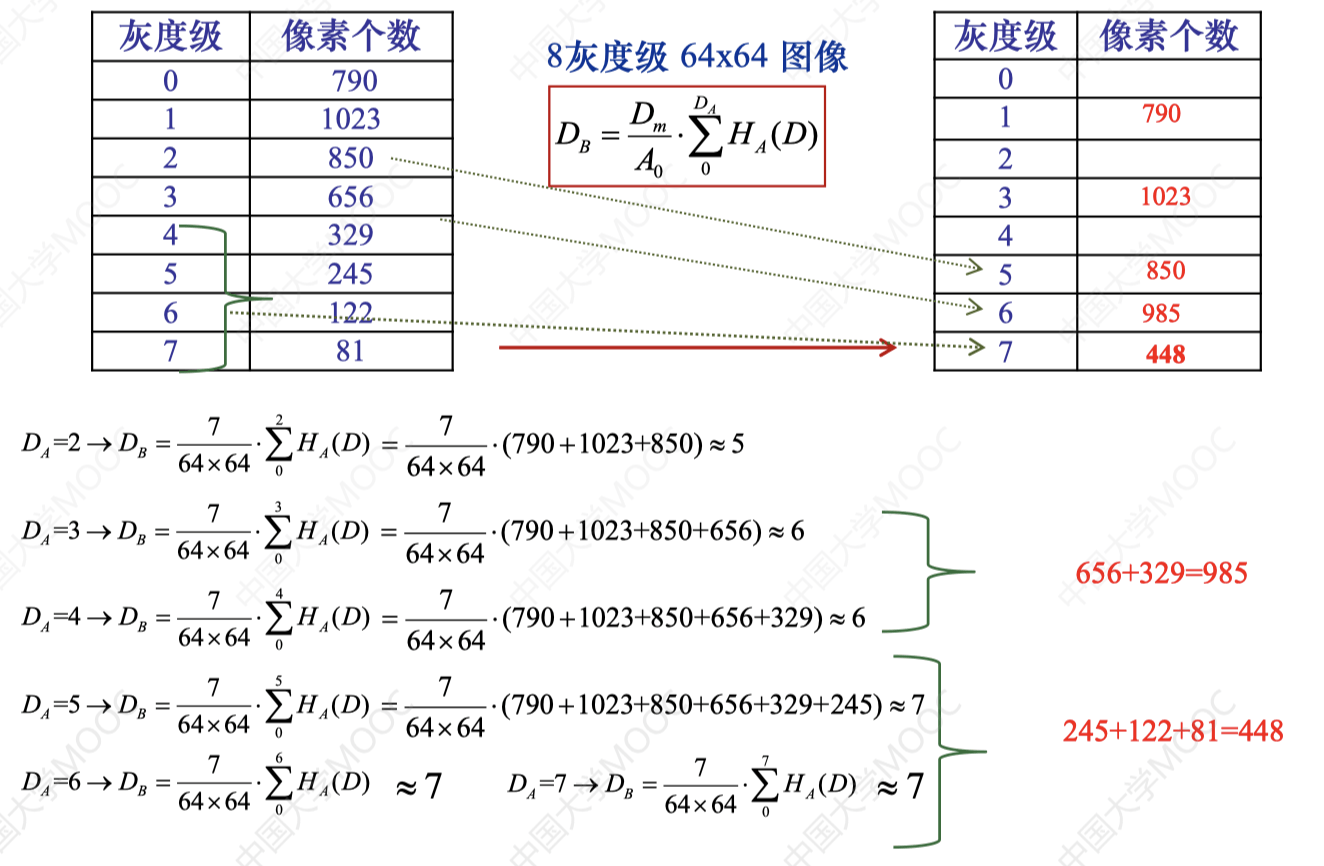
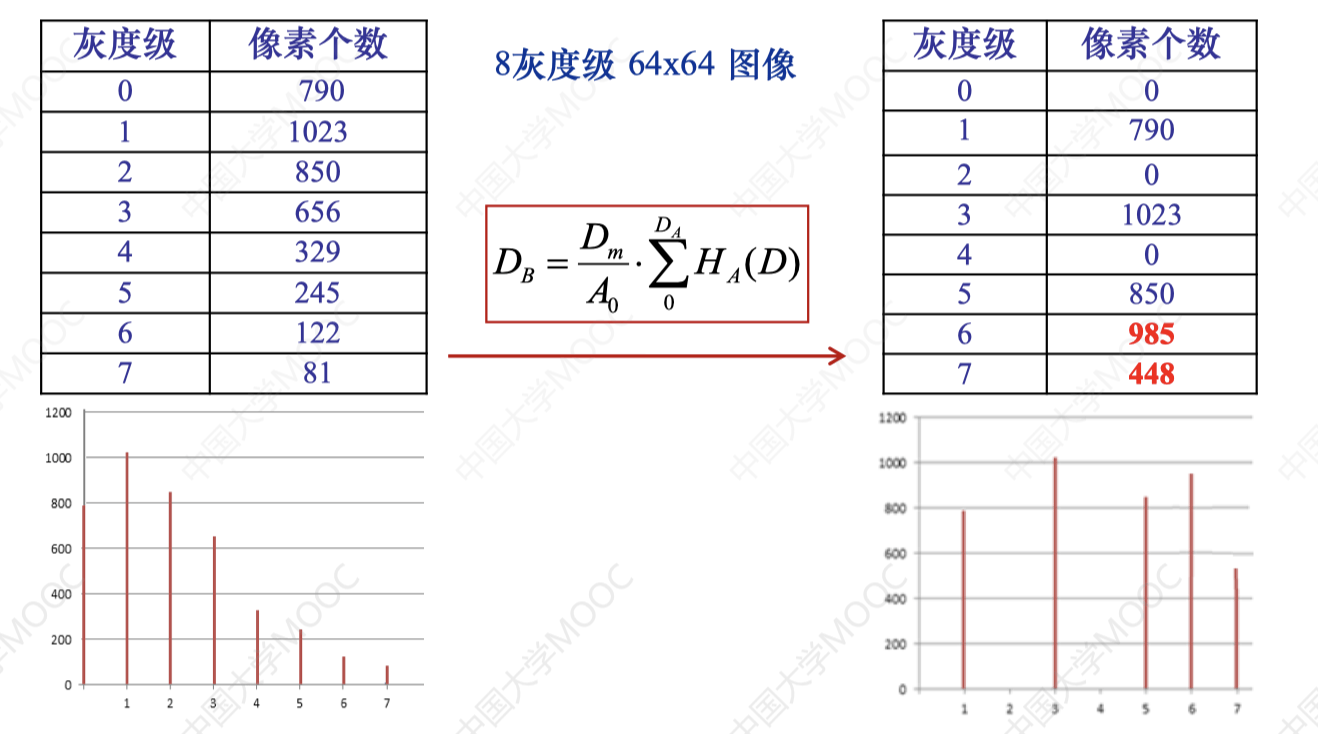
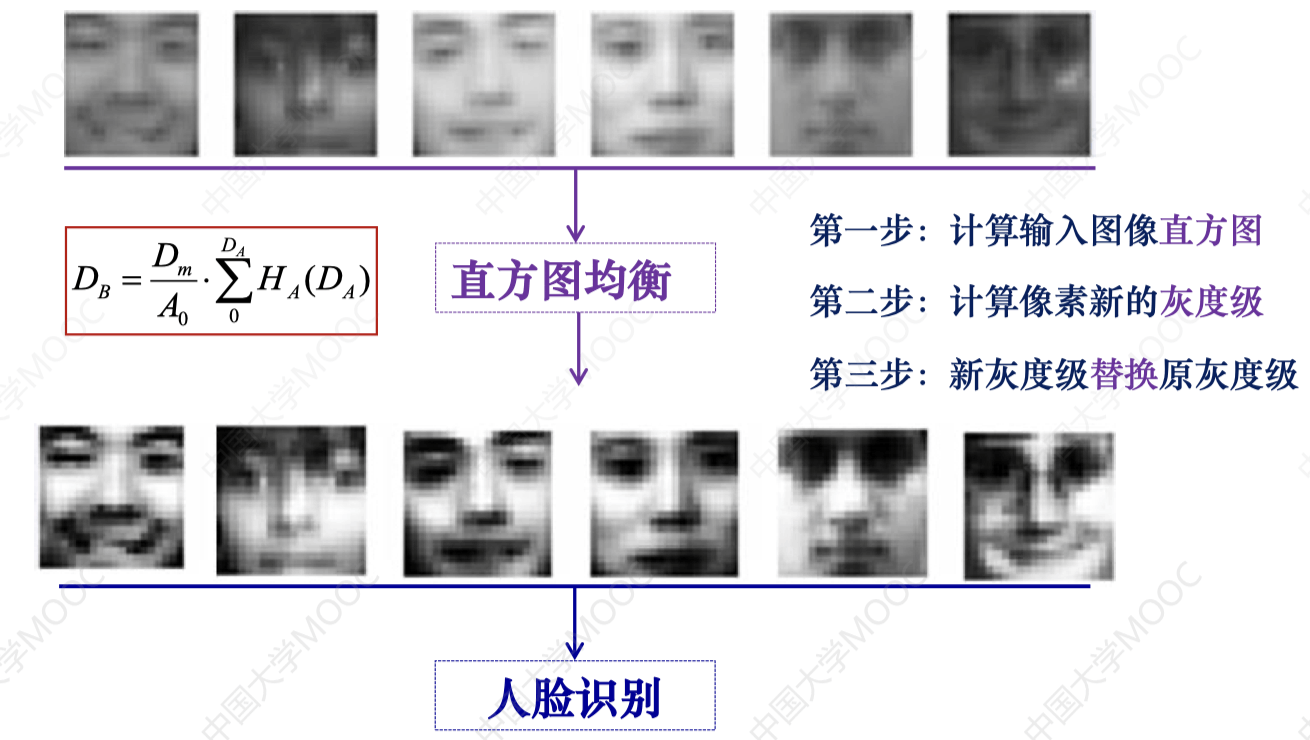
3. 直方图均衡应用
4. 参考








