Proximal Policy Optimization (PPO)

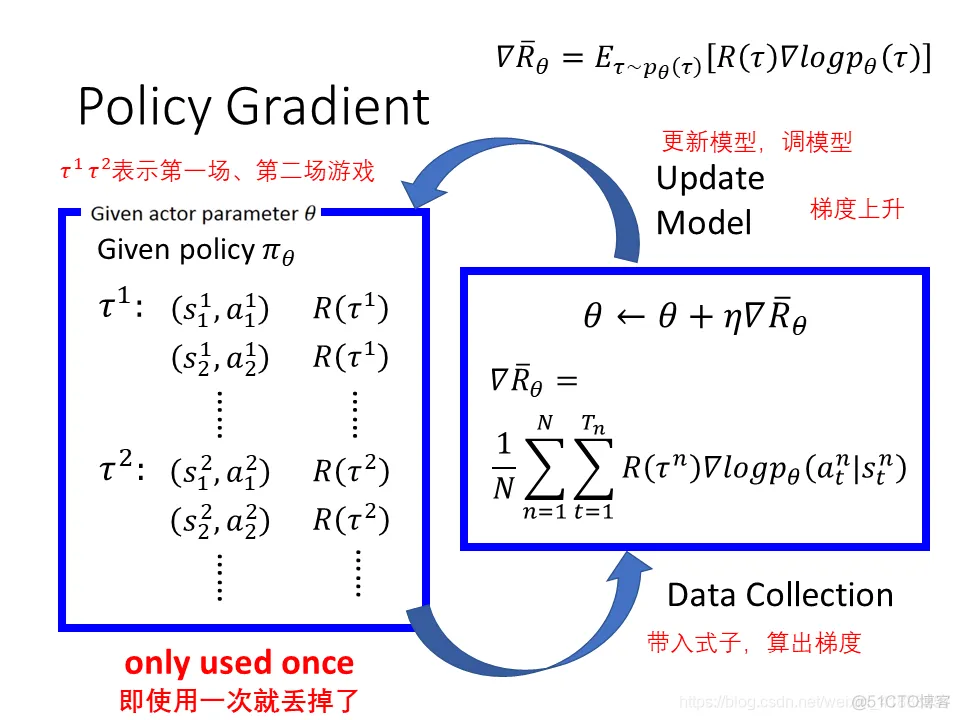
Policy Gradient

$$\tau=\left\{s_1, a_1, s_2, a_2, \cdots, s_T, a_T\right\}$$

当参数是$\theta$的时候某一个 trajectory 回合里面发生$\tau$的几率：

$$\begin{aligned} p_\theta(\tau)& =p\left(s_1\right) p_\theta\left(a_1 \mid s_1\right) p\left(s_2 \mid s_1, a_1\right) p_\theta\left(a_2 \mid s_2\right) p\left(s_3 \mid s_2, a_2\right) \cdots \\ & =p\left(s_1\right) \prod_{t=1}^T p_\theta\left(a_t \mid s_t\right) p\left(s_{t+1} \mid s_t, a_t\right) \\ & \end{aligned}$$

Expect Reward，穷举所有的Trajectory不同回合的Reward乘以不同回合的几率再求和就是期望Reward

$$\bar{R}_\theta=\sum_\tau R(\tau) p_\theta(\tau)=E_{\tau \sim p_\theta(\tau)}[R(\tau)]$$

要求期望Reward最大值采用梯度上升

$$\begin{aligned} \nabla \bar{R}_\theta&=\sum_\tau R(\tau) \nabla p_\theta(\tau)=\sum_\tau R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}\\ &=\sum_\tau R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau)\\ &=E_{\tau \sim p_\theta(\tau)}\left[R(\tau) \nabla \log p_\theta(\tau)\right] \approx \frac{1}{N} \sum_{n=1}^N R\left(\tau_n\right) \nabla \log p_\theta\left(\tau_n\right) \end{aligned}$$

由于env的那部分$p\left(s_{t+1} \mid s_t, a_t\right)$和无关$\theta$，所以无需对其做 gradient，只需要对actor的那部分$p_\theta\left(a_t \mid s_t\right)$做gradient，所以：

$$\nabla \bar{R}_\theta=\frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} R\left(\tau_n\right) \nabla \log p_\theta\left(a_t^n \mid s_t^n\right)$$

这里为什么要用一个log呢？（也就是为什么要多一个再除以p的操作）直接对p取梯度不好吗？因为如果动作a很好但是很罕见，而动作b很多但是不太好，但是在求和操作的时候，就会把b的Reward求和变得很大，为了使得目标函数最大，模型就会偏好出现几率较高action b，而这不是我们想要的。除以p的操作就是一个标准化的操作，出现次数越多也就是概率越大，除以自己就标准化了

On-policy -> Off-policy

• On-policy: The agent learned and the agent interacting with the environment is the same.

• Off-policy: The agent learned and the agent interacting with the environment is different.

前面的policy gradient的做法就是on-policy，即要learn的policy和与环境互动的policy是同一个。当update参数以后,从$\theta$变成$\theta'$,那么之前sample出来的data就不能用了。Update一次参数，只能做一次gradient acent，而后再去 collect data，非常耗时，所以需要 off policy。off-policy可以拿一批data用好几次。

Importance Sampling

从分布p中采样x，当p无法积分，那就约等于右边的均值

$$E_{x \sim p}[f(x)] \approx N \sum_{i=1}^N f\left(x^i\right)$$

假设：无法从p中采样data，只能从q中采样data，那么这个等式无法近似

$$E_{x \sim p}[f(x)]=\int f(x) p(x) d x=\int f(x) \frac{p(x)}{q(x)} q(x) d x=E_{x \sim q}\left[f(x)\left[\frac{p(x)}{q(x)}\right]\right.$$

变成从q 分布中采样data，$\displaystyle{\frac{p(x)}{q(x)}}$相当于修正权重

Issue of Importance Sampling

期望相同，但是方差不同

$$V A R[X] { =E[X^{2}]-(E[X])^{2}}$$

$f(x)$的方差

$$\operatorname{Var}_{x\sim p}[f(x)]=E_{x\sim p}[f(x)^{2}]-\left(E_{x\sim p}[f(x)]\right)^{2}$$

$f(x)\displaystyle{\frac{p(x)}{q(x)}}$的方差

$$\begin{aligned} Var_{x\sim q}[f(x)\displaystyle{\frac{p(x)}{q(x)}}]&=E_{x\sim q}\left[\left(f(x)\displaystyle{\frac{p(x)}{q(x)}}\right)^{2}\right]-\left(E_{x\sim q}\left[f(x)\displaystyle{\frac{p(x)}{q(x)}}\right]\right)^{2}\\ &={E_{x\sim p}\left[f(x)^{2}\displaystyle{\left[\displaystyle{\frac{p(x)}{q(x)}}\right]}- (E_{x\sim p}[f(x)]\right)^{2}} \end{aligned}$$

方差主要差别在第一项，也就是$\displaystyle{\frac{p(x)}{q(x)}}$的值。所以如果p和q差很多，而且采样不够多，区别就差很大。当然，如果sample次数足够多，那么期望相同，也没有太大区别。

Off-policy

$$\nabla \bar{R}_\theta=E_{\tau \sim p_{\theta^{\prime}}(\tau)}\left[\frac{p_\theta(\tau)}{p_{\theta^{\prime}}(\tau)} R(\tau) \nabla \log p_\theta(\tau)\right]$$

$\theta'$ sample一次data,可以给 $\theta$ uptake很多次,完了以后再去 Sample data

Add Constraint

Actor-Critic

减小Actor的方差：Causality方法

策略梯度的公式变为

$$\nabla J(\theta)=\frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{T}\nabla_\theta log\pi_\theta(a_{i,t}|s_{i,t})(\sum_{t'=t}^{T}r(s_{i,t'},a_{i,t'}))$$

即后一项关于的奖励的累加只累加当前时间步$t$之后的奖励，直观的理解是$t'$时刻策略的改变不会影响到$t'$之前时间步的奖励

在上式中，对$\sum_{t=1}^{T}\nabla_\theta log\pi_\theta(a_{i,t}|s_{i,t})$使用的是Monte Carlo估计方法，这种方法方差大。将该项可以写成$\hat{Q}_{i}(s_t,a_t)$，Q值代表未来的累计奖励的期望，可以使用值函数近似的方法来估计$\hat{Q}_{i}(s_t,a_t)$ ，从而进一步减少方差。

$$\nabla J(\theta)=\frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{T}\nabla_\theta log\pi_\theta(a_{i,t}|s_{i,t})\hat{Q}_{i}(s_t,a_t)$$

Baseline方法

如果希望在上式的基础上，进一步减少方差，那么可以为$\hat{Q}_{i}(s_t,a_t)$ 添加baseline ，将baseline记为$b$，则策略梯度的公式为

$$\nabla J(\theta)=\frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{T}\nabla_\theta log\pi_\theta(a_{i,t}|s_{i,t})(\hat{Q}(s_t,a_t)-b)$$

可以证明，只有在$b$与动作$a_t$无关的情况下，上述改进才与之前的策略梯度公式等价。$b$一般选择为状态$s_t$的值函数（还与$\theta$有关？），即$b=\hat{v}_i(s)$ 。

当baseline是状态值函数时，策略梯度可以写成

$$\nabla J(\theta)=\frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{T}\nabla_\theta log\pi_\theta(a_{i,t}|s_{i,t})(\hat{Q}(s_t,a_t)-\hat{V}(s_t))$$

其中， $\hat{Q}(s_t,a_t)-\hat{V}(s_t)=\hat{A}(s_t,a_t)$称为Advantage Function，其中

$$Q(s_t,a_t)=r(s_t,a_t)+\sum_{s_{t+1}}P(s_{t+1}|s_t,a_t)[V(s_{t+1})]$$

如果不考虑状态转移概率，用采样的方式来估计状态转移，则在当前策略参数下，

$$Q(s_t,a_t)\approx r(s_t,a_t)+V(s_{t+1})$$

因此策略梯度公式可以进一步写成

$$\nabla J(\theta)=\frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{T}\nabla_\theta log\pi_\theta(a_{i,t}|s_{i,t})(r(s_t,a_t)+\hat{V}(s_{t+1})-\hat{V}(s_t))$$

在上式中，我们需要估计状态值函数$\hat{V}(s_t)$的值。用于估计$\hat{V}(s_t)$的部分被称为Critic。

Actor-Critic的基本流程为：

$$采样\rightarrow 更新Critic参数\rightarrow 根据Critic计算Advantage Function \rightarrow 更新Actor参数$$

参考

https://blog.51cto.com/u_15721703/5575736

https://www.zhihu.com/question/56692640/answer/289913574

[https://danieltakeshi.github.io/2017/03/28/going-deeper-into-reinforcement-learning-fundamentals-of-policy-gradients/](