神经网络训练

General Guidance

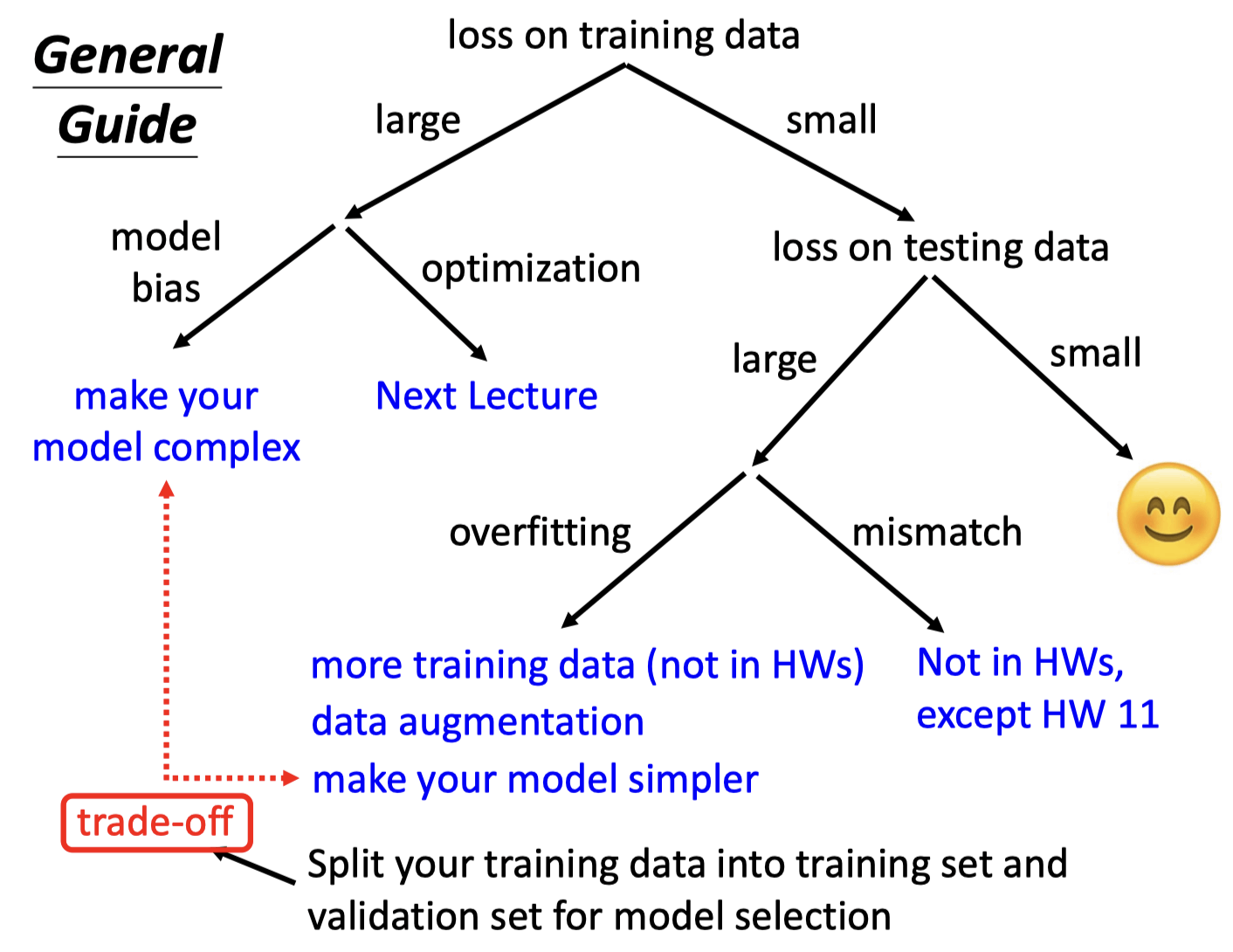
Model Bias

• The model is too simple.

  find a needle in a haystack, but there is no needle

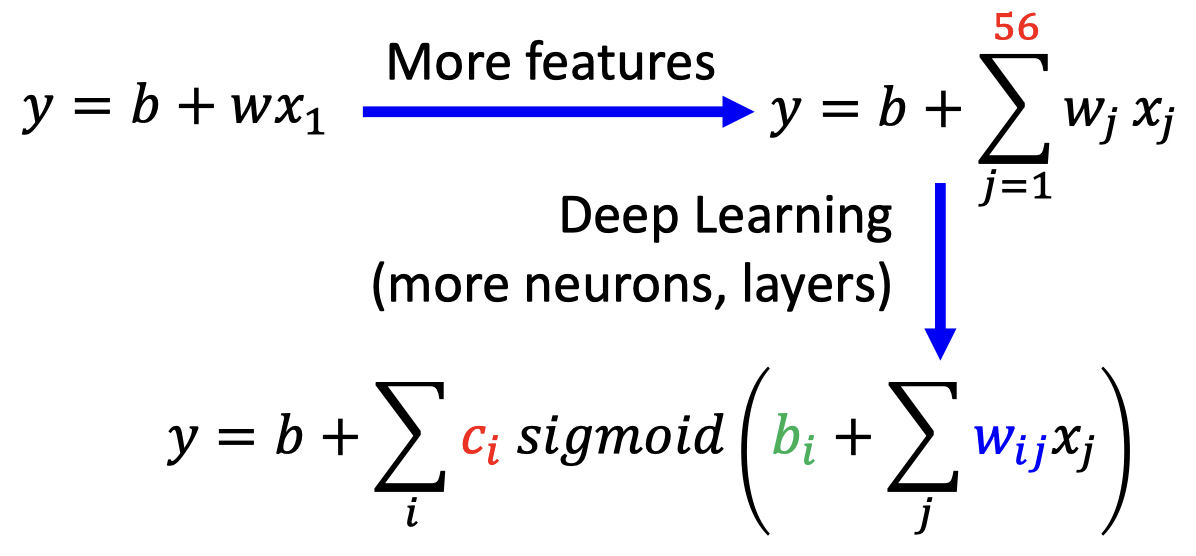
• Solution: redesign your model to make it more flexible

  1. More features
  2. Deep Learning (more neurons, layers)

Optimization Issue

A needle is in a haystack, just cannot find it.

Model Bias v.s. Optimization Issue

怎么区分？

• Start from shallower networks (or other models), which are easier to optimize.

• If deeper networks do not obtain smaller loss on training data, then there is optimization issue.

• Solution: More powerful optimization technology

Overfitting

• Small loss on training data, large loss on testing data.

• Solution

  1. More training data

  2. Data augmentation

     图片翻转、放大（不能颠倒）

  3. constrained model

     Less parameters, sharing parameters(CNN), Less features, Early stopping, Regularization, Dropout

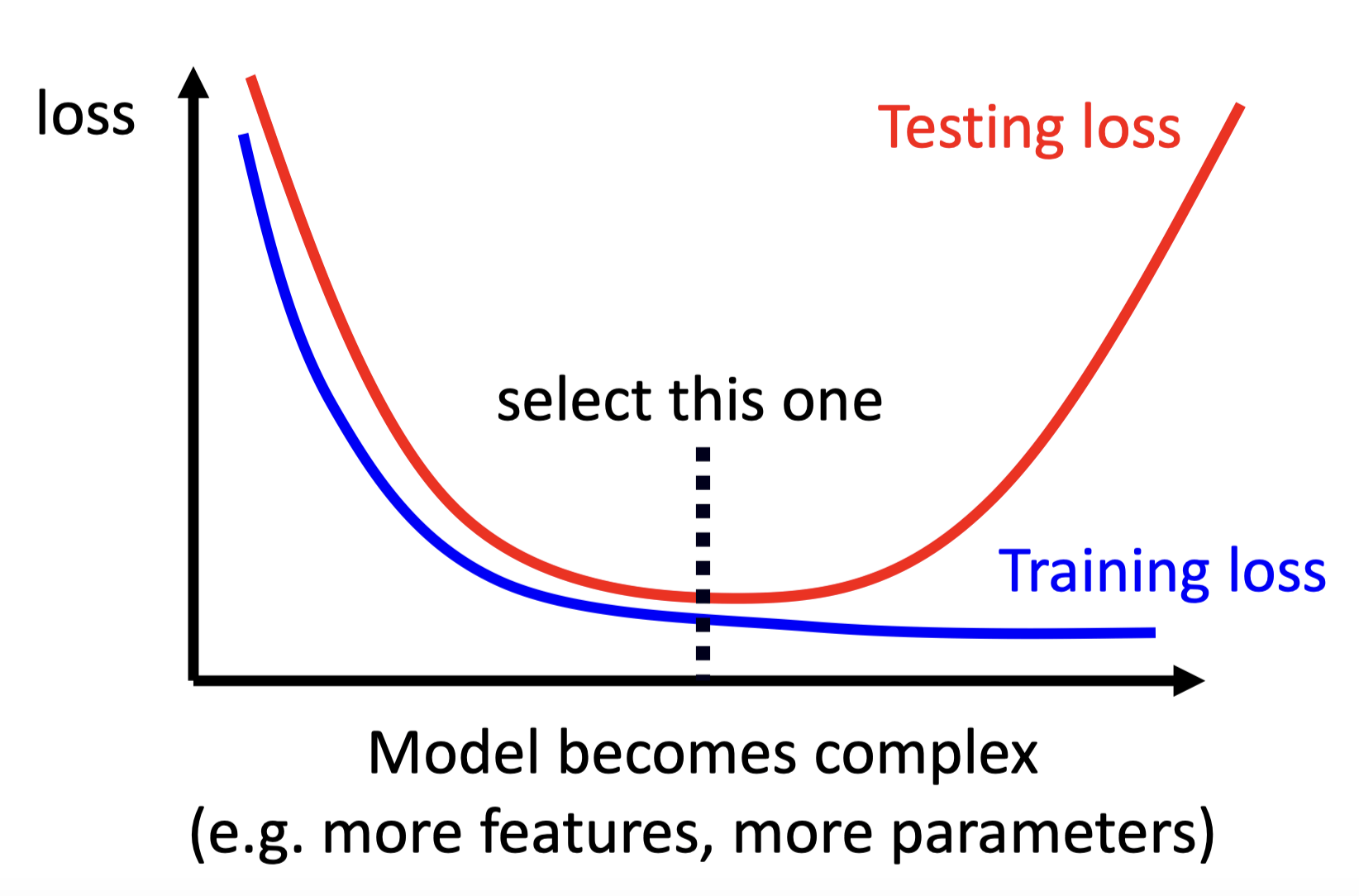
Bias-Complexity Trade-off

Mismatch

• Your training and testing data have different distributions. Be aware of how data is generated.

Gradient is small

Optimization Fails

• gradient is close to zero (critical point)
  1. local minima
  2. saddle point

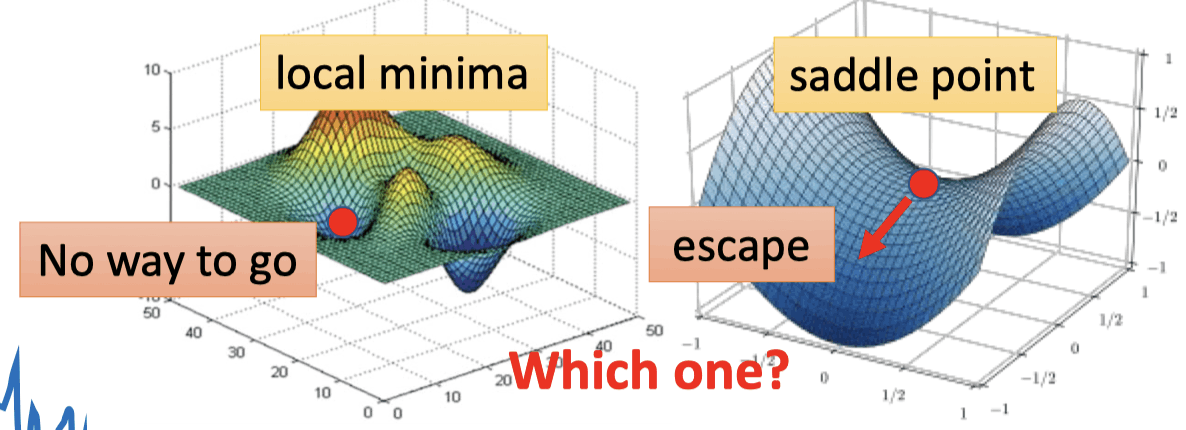
区分local minima和saddle point

• Tayler Series Approximation

在critical point，gradient为0，不考虑第二项

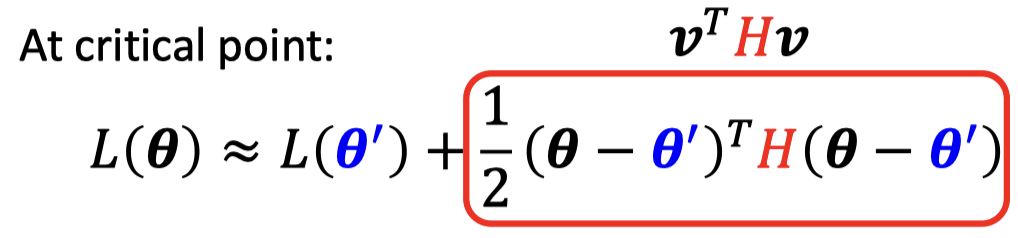
• Example

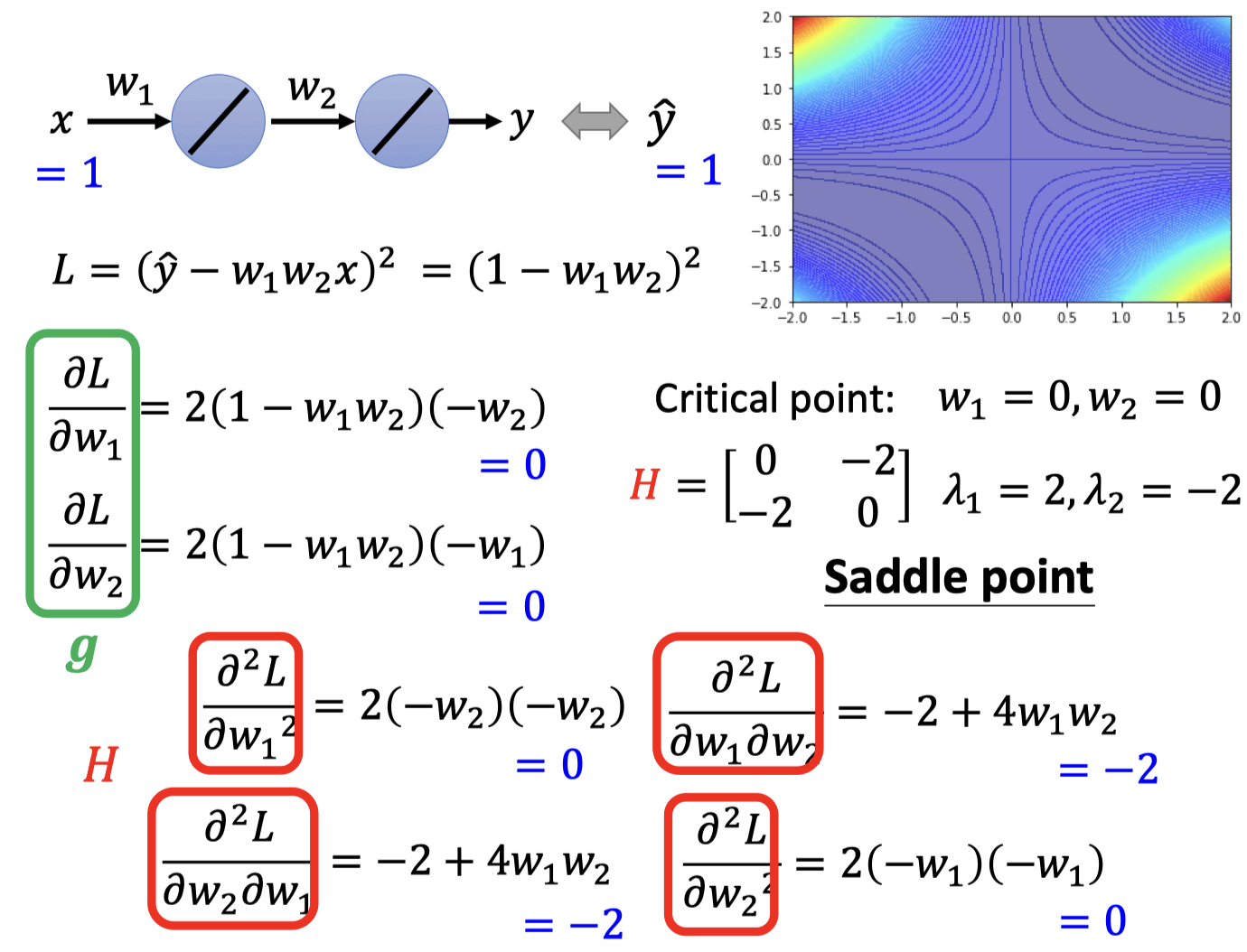
Saddle point更新参数

𝐻 may tell us parameter update direction

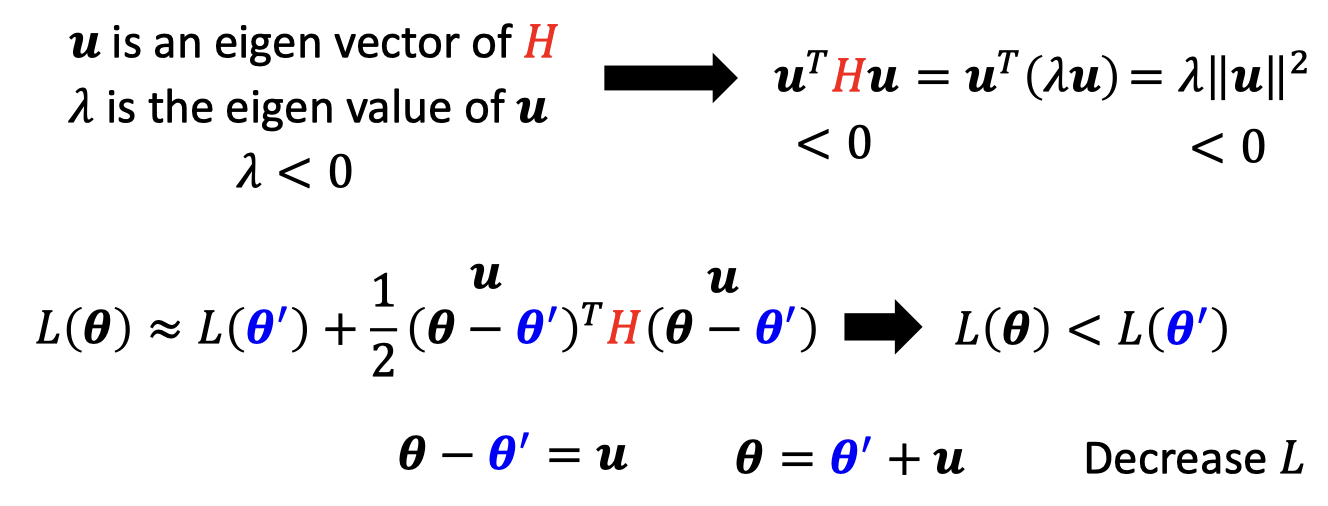
找到H负的eigen value $\lambda$对应的eigen vector $\mu$，用这个eigen vector更新 $\theta = \theta'+\mu$，Loss就会下降

Update the parameter along the direction of $\mu$ You can escape the saddle point and decrease the loss.(this method is seldom used in practice，计算量大)

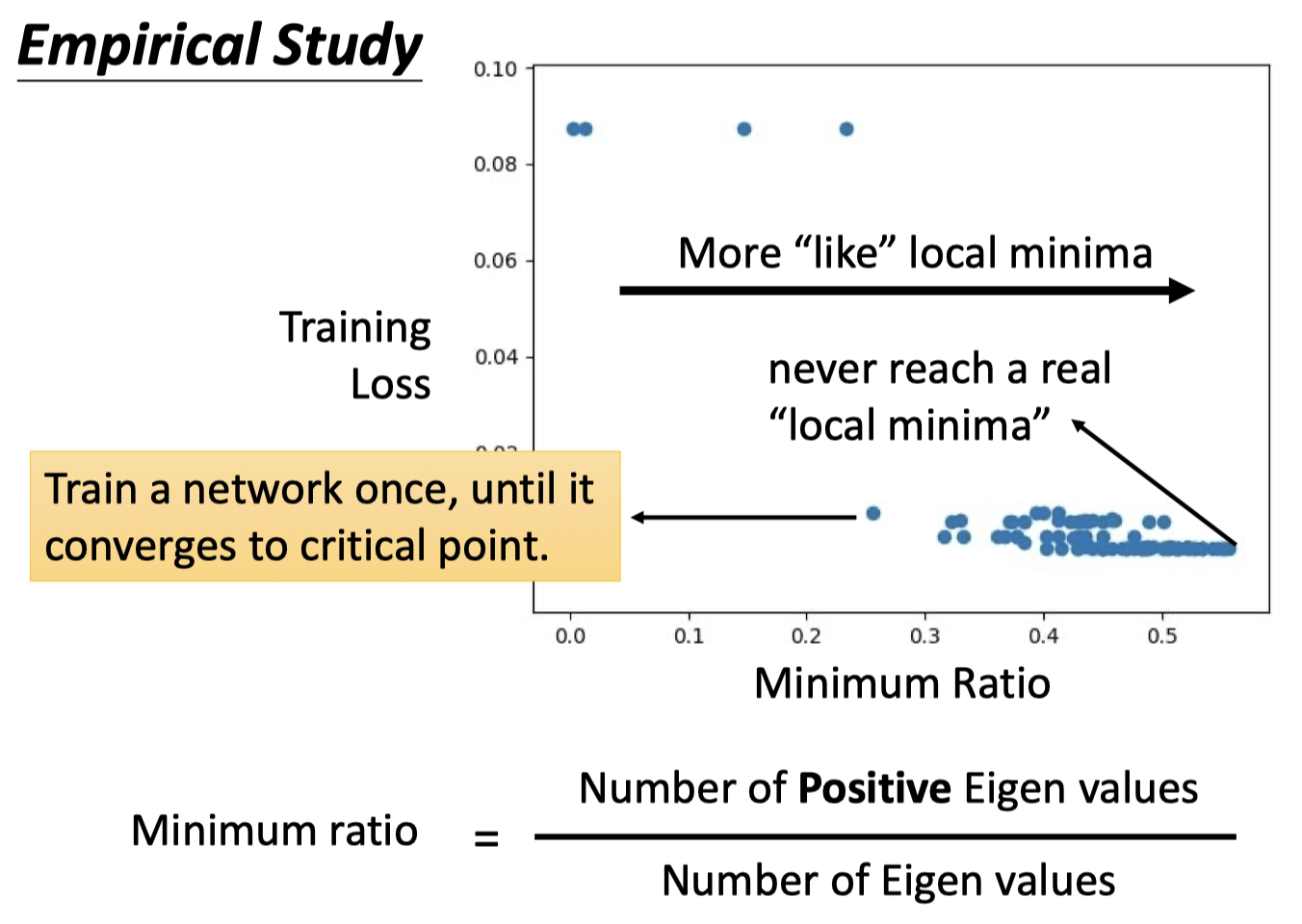
大部分情况，loss无法下降是卡在saddle point（一部分eigen value为正，一部分为负）

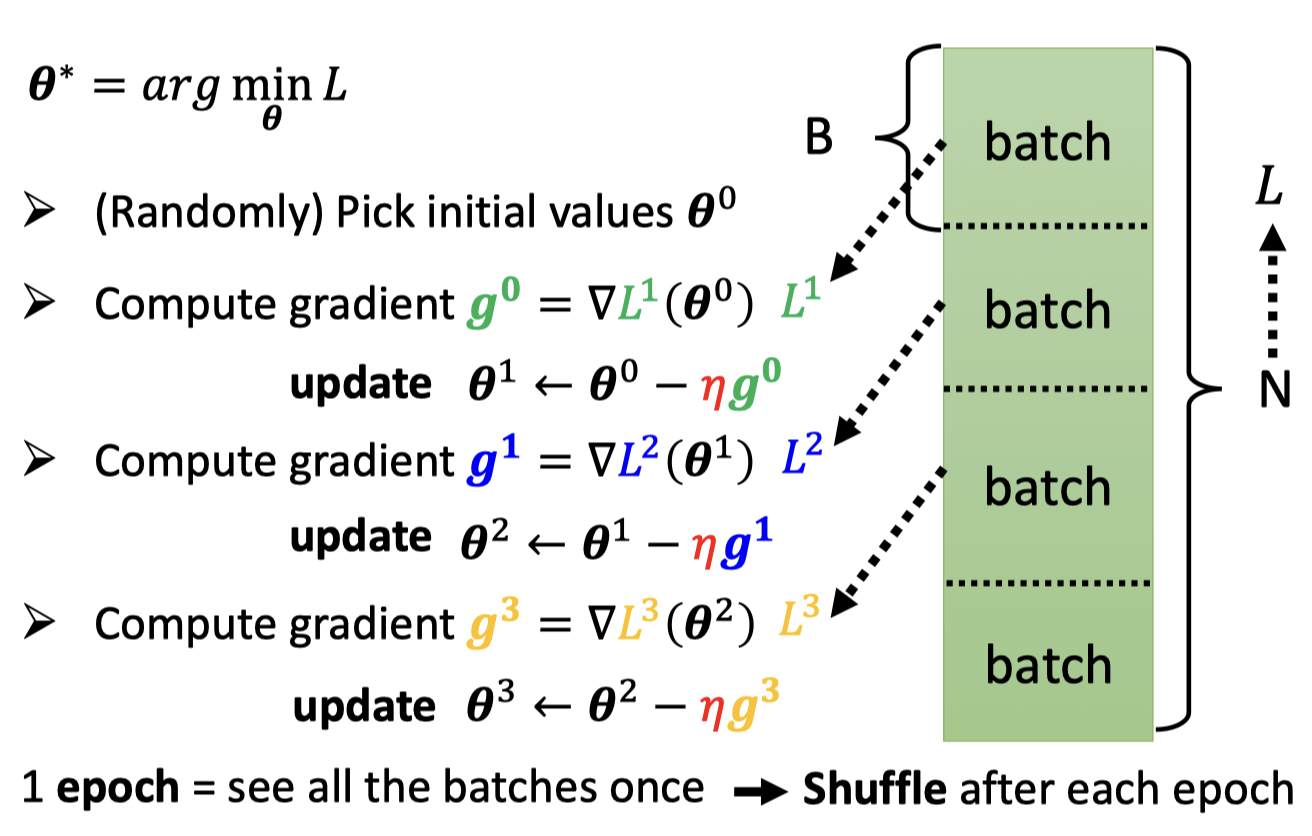
Batch

Optimization with Batch

每个batch更新一次参数

Small Batch v.s. Large Batch

• Smaller batch requires longer time for one epoch (longer time for seeing all data once) (Parallel computing)

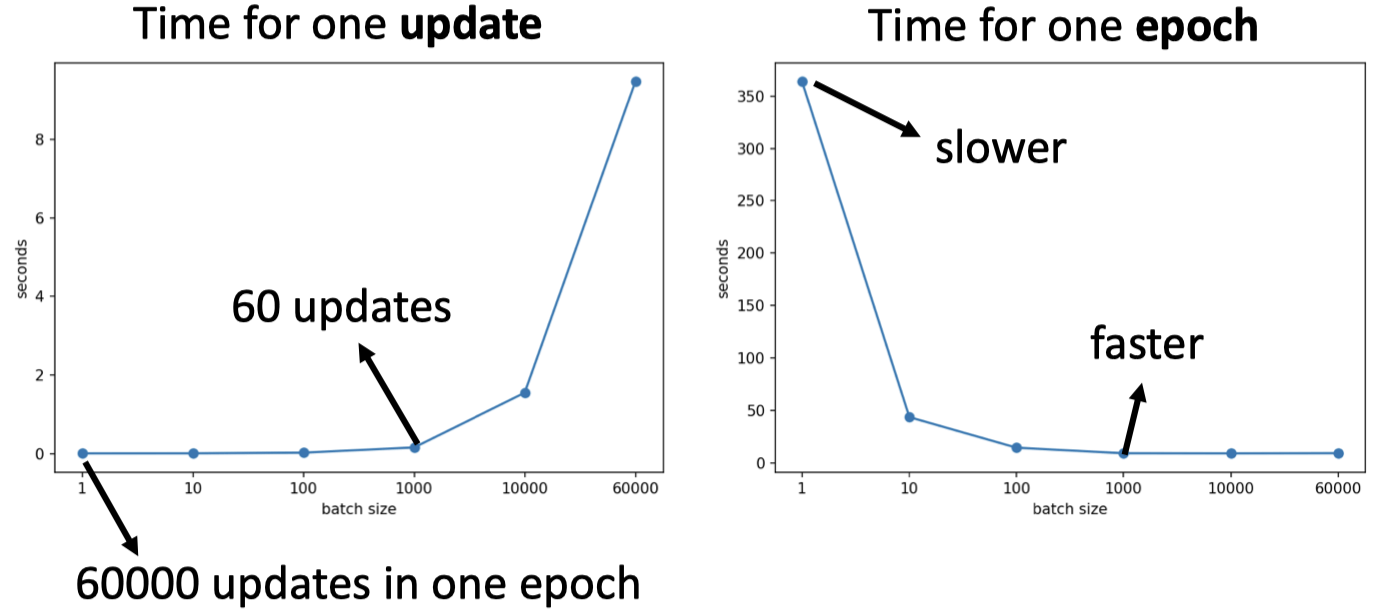
• Batch size 越大，准确率越低

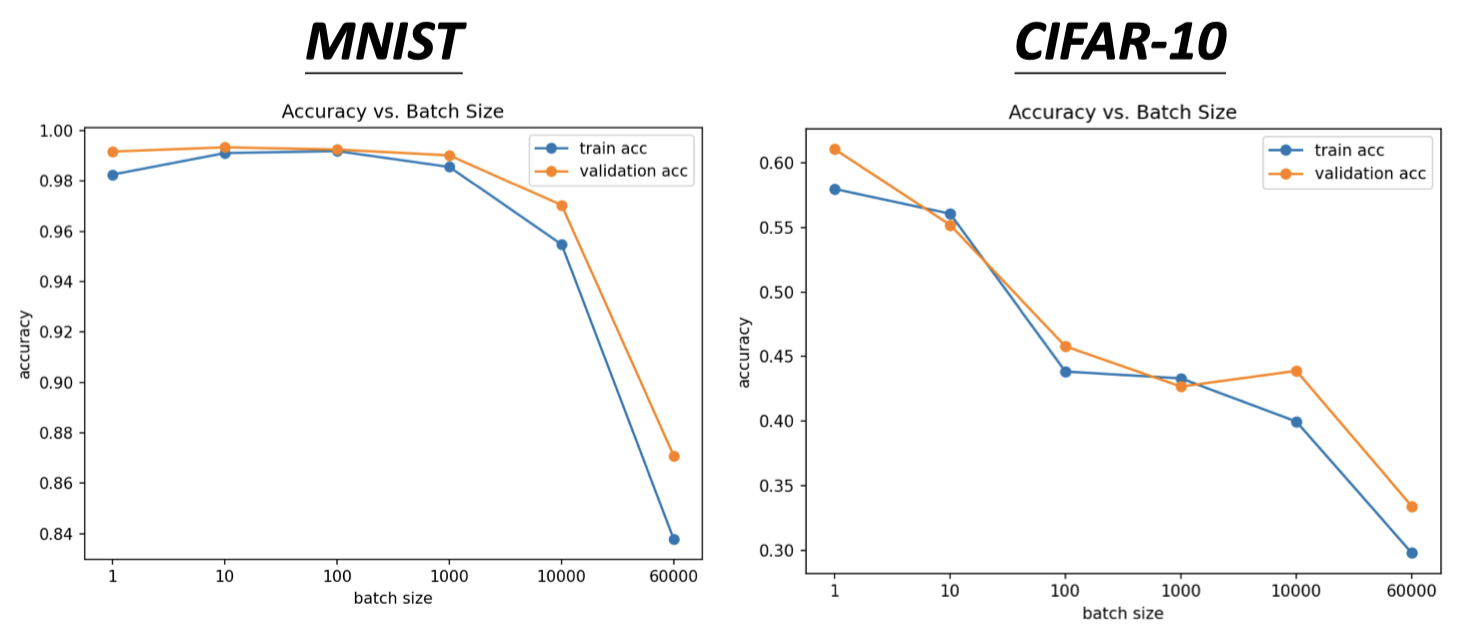
Smaller batch size has better performance. “Noisy” update is better for training

每一次batch更新参数，loss函数都是略有差异的

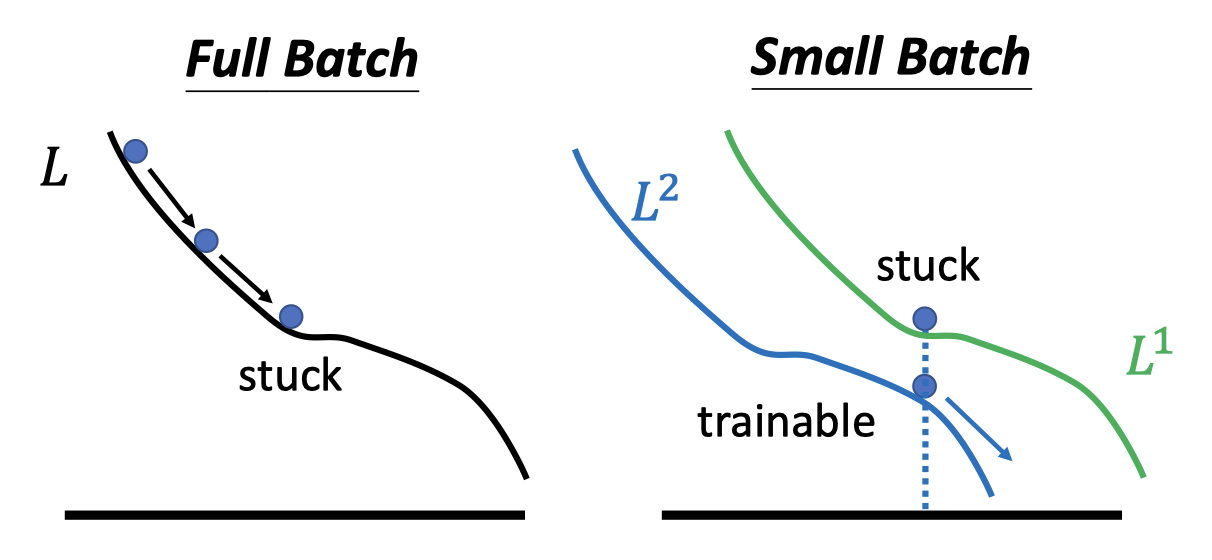
• Small batch is better on testing data? (better generalization)

  On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima https://arxiv.org/abs/1609.04836

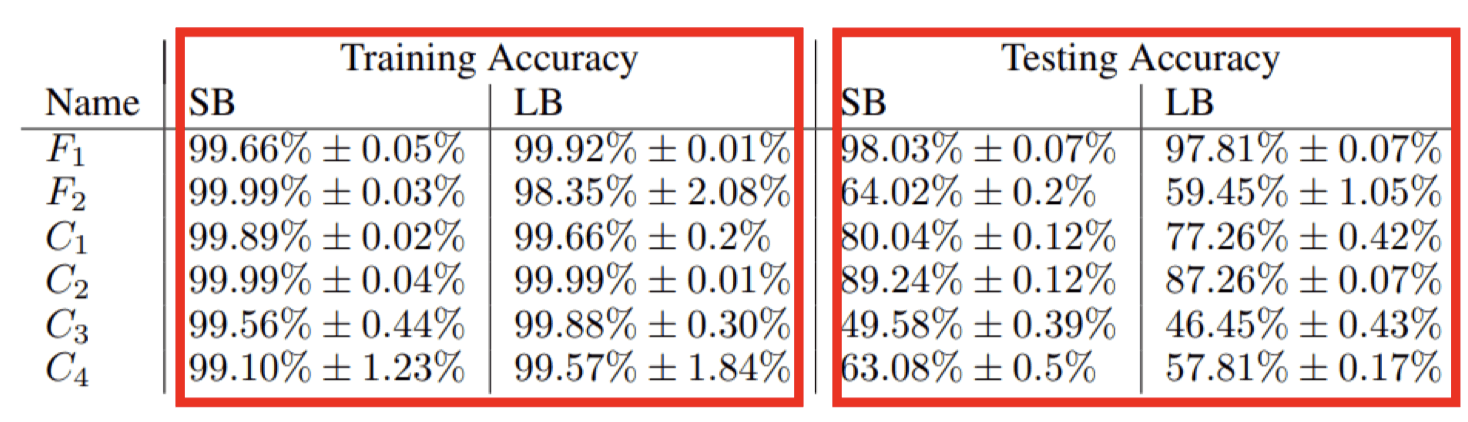
Batch size is a hyperparameter you have to decide.

• 全都要？

  • Large Batch Optimization for Deep Learning: Training BERT in 76 minutes (https://arxiv.org/abs/1904.00962)

  • Extremely Large Minibatch SGD: Training ResNet-50 on ImageNet in 15 Minutes (https://arxiv.org/abs/1711.04325)

  • Stochastic Weight Averaging in Parallel: Large-Batch Training That Generalizes Well (https://arxiv.org/abs/2001.02312)

  • Large Batch Training of Convolutional Networks (https://arxiv.org/abs/1708.03888)

  • Accurate, large minibatch sgd: Training imagenet in 1 hour (https://arxiv.org/abs/1706.02677)

Momentum

• 球从高处滚下来

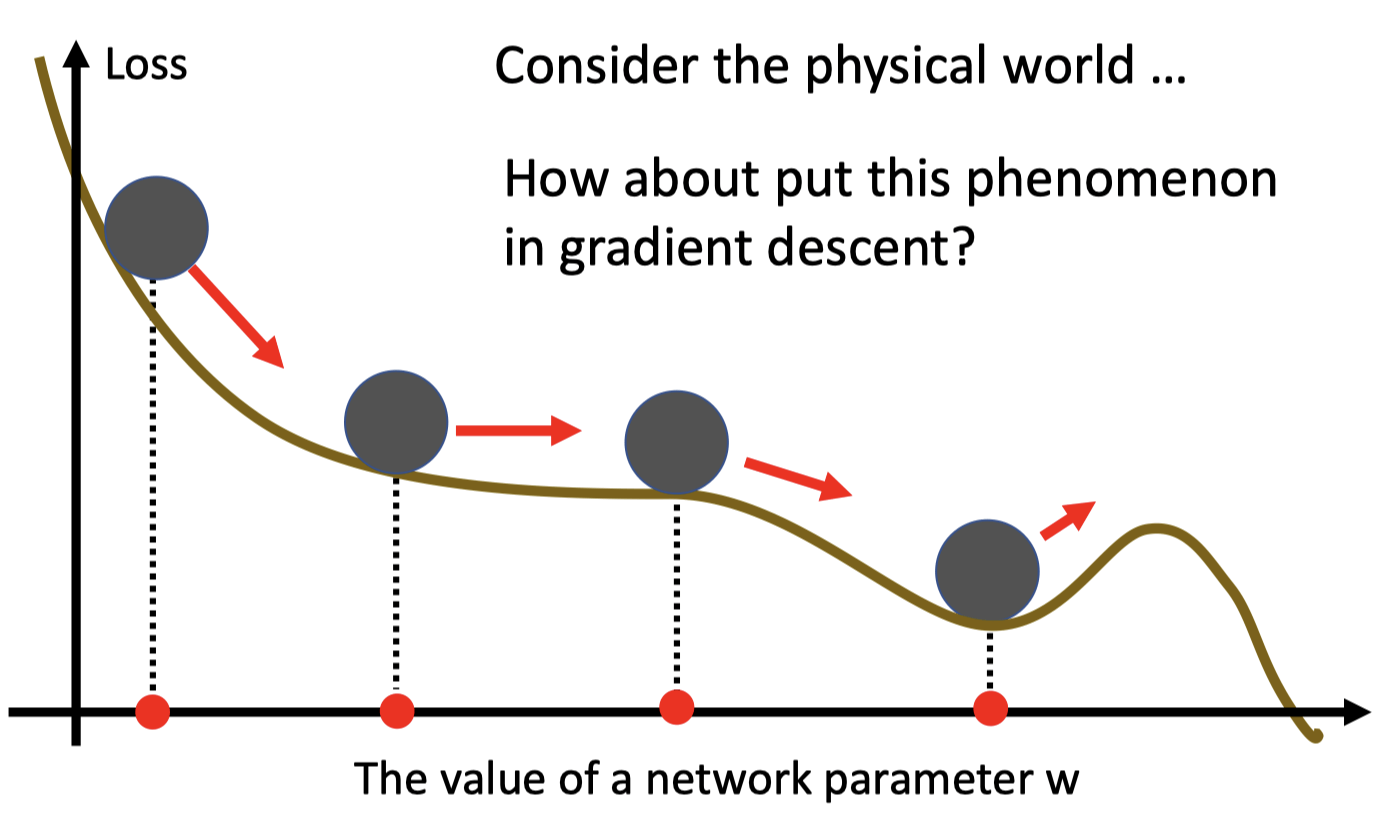
Gradient Descent + Momentum

每一步的移动 = 上一次的移动 - gradient

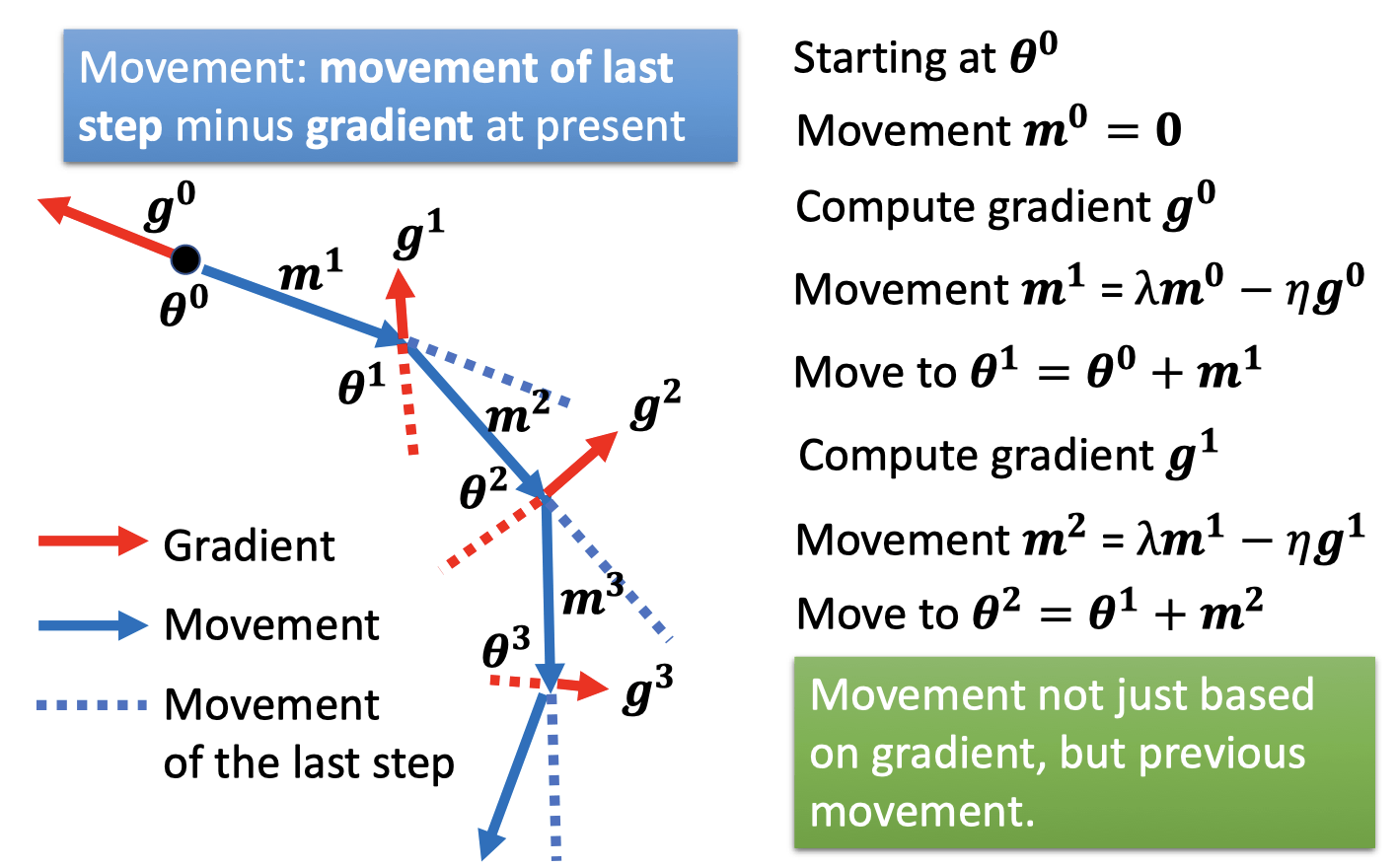
$m^{i}$ is the weighted sum of all the previous gradient: $g^{0},\,g^{1},\,\ldots,\,g^{i-1}$

$${ {m^{0}=0} }\\ { {m^{1}=-\eta g^{0} }}\\ m^{2}=-\lambda\eta g^{0}-\eta g^{1}$$

Movement not just based on gradient, but previous movement.

Adaptive Learning Rate

• Training stuck ≠ Small Gradient

  可能在error surface的山谷来回震荡

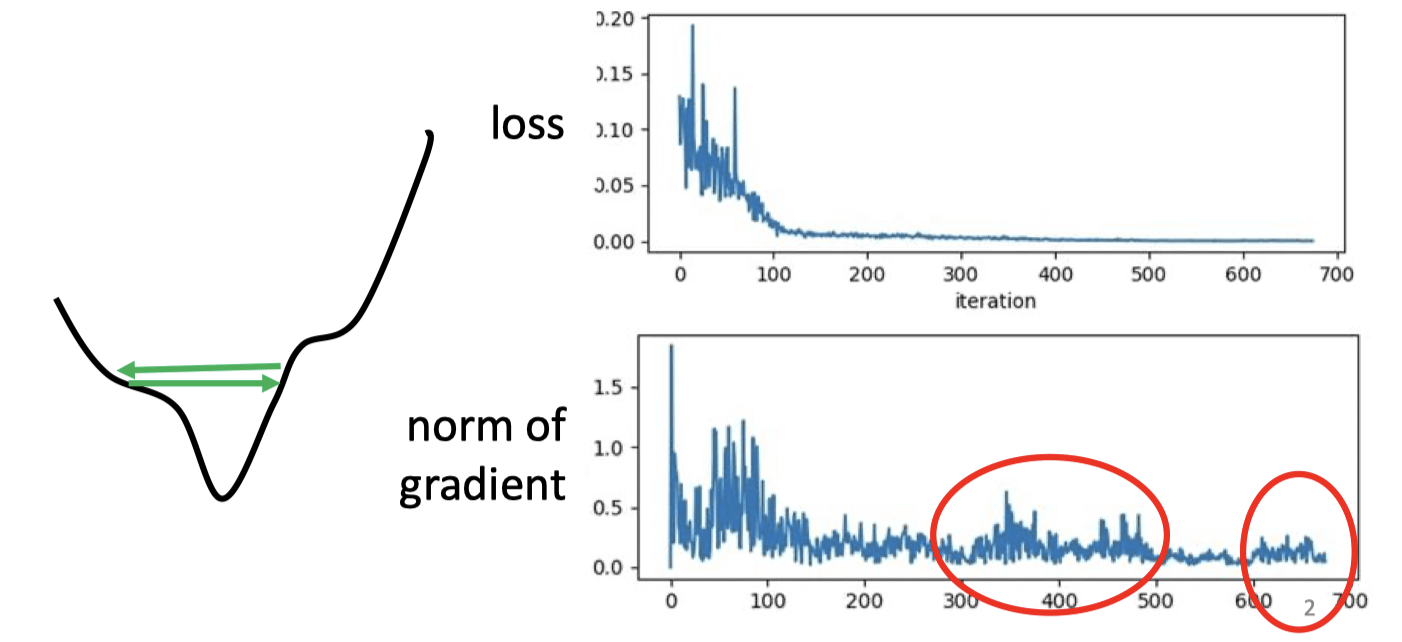
Different parameters needs different learning rate

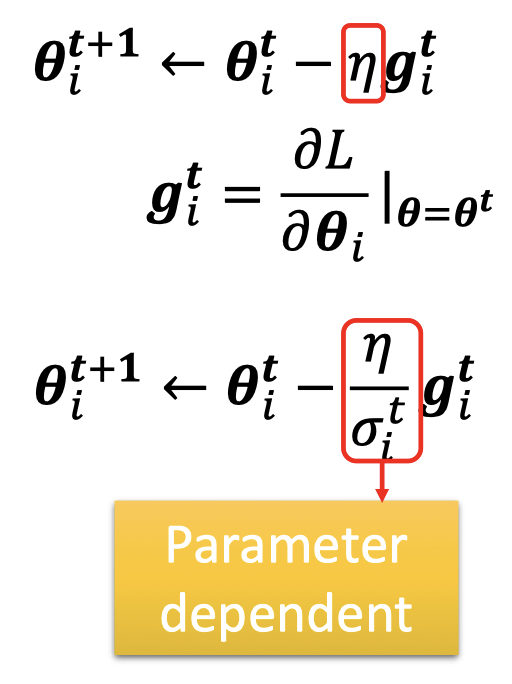
• Root Mean Square

  $\sigma$ 是所以gradient的平方的平均开根号

$$\theta_{i}^{t+1} \rightarrow\theta_{i}^{t}-\frac{\eta}{\sigma_{i}^{t} }g_{i}^{t}\\ { {\sigma_{i}^{t}=\sqrt{\frac{1}{t+1}\displaystyle\sum_{i=0}^{t}(g_{i}^{t})^{2} }} }$$

error surface越平滑，$\sigma$ 越小，$\theta$ 更新越大。rror surface越陡，$\sigma$ 越大，$\theta$ 更新越小。

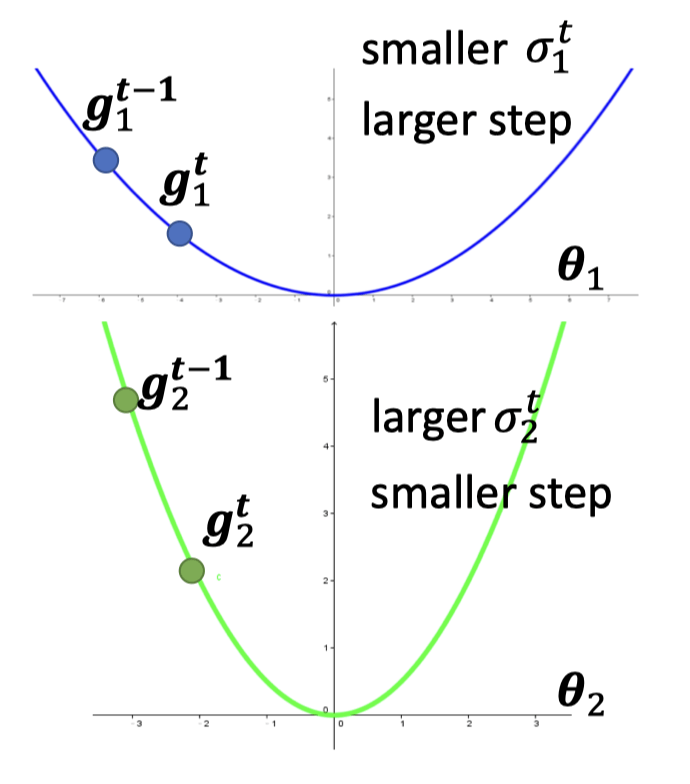
Learning rate adapts dynamically

Root Mean Square 不能根据当前 error surface 的情况快速地及时变化

• RMSProp

  $\sigma$ 是之前的 $\sigma$ 和这次的gradient加权

  The recent gradient has larger influence, and the past gradients have less influence.

$$\theta_{i}^{t+1} \rightarrow\theta_{i}^{t}-\frac{\eta}{\sigma_{i}^{t} }g_{i}^{t}\\ \sigma_{i}^{t}={\sqrt{\alpha{\left(\sigma_{i}^{t-1}\right)}^{2}+{(1-\alpha)\left({g_{i}^{t} }\right)}^{2} }}$$

• Adam: RMSProp + Momentum

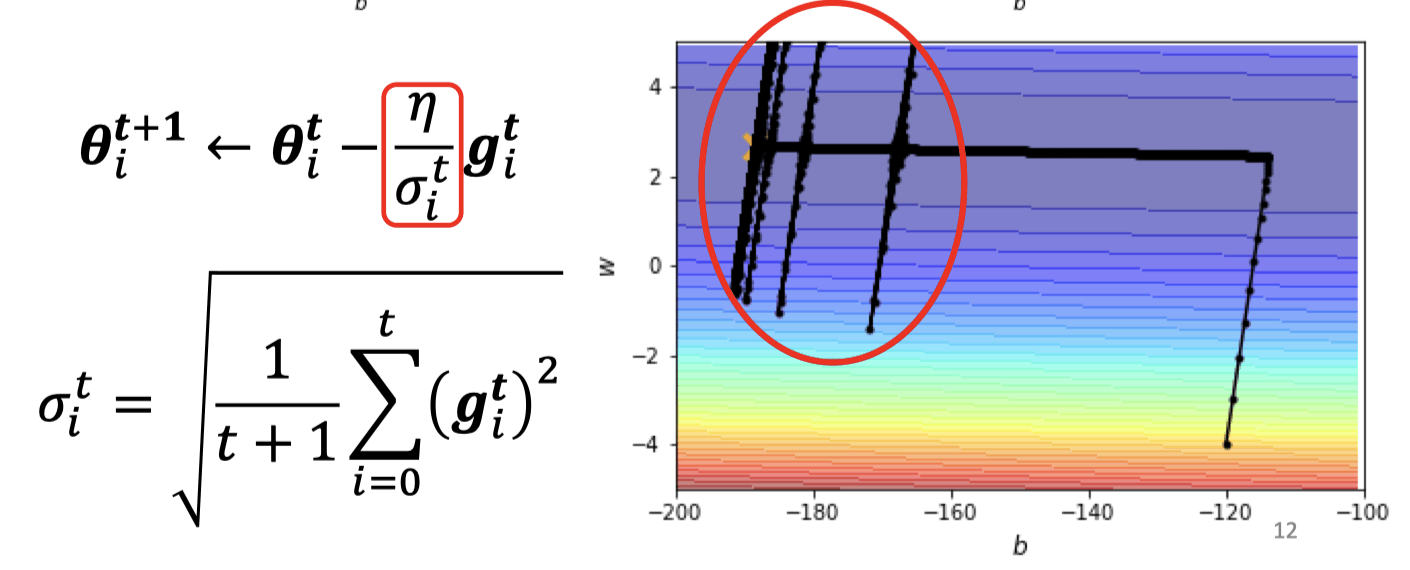
红圈里因为$\sigma$很小，会突然跳很远

Learning Rate Scheduling

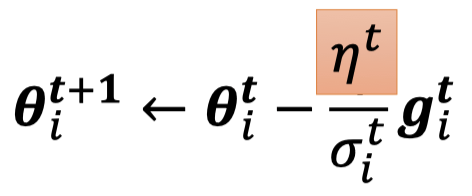
1. Learning Rate Decay

   As the training goes, we are closer to the destination, so we reduce the learning rate.

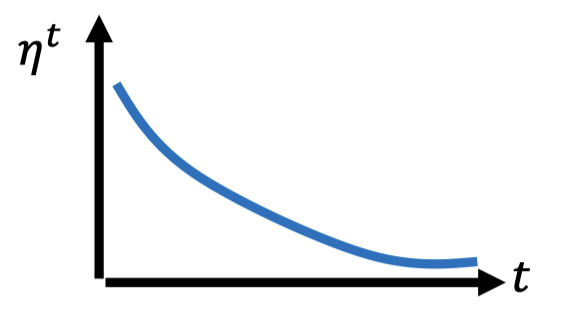
2. Warm Up （黑科技）

   Increase and then decrease?

   了解更多：RAdam: https://arxiv.org/abs/1908.03265

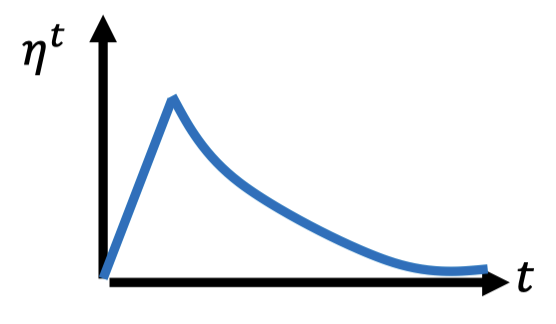
• Residual Network: https://arxiv.org/abs/1512.03385
• Transformer: https://arxiv.org/abs/1706.03762

Summary of Optimization

• (Vanilla) Gradient Descent

$$\theta_{i}^{t+1} \leftarrow\theta_{i}^{t}-\eta g_{i}^{t}$$

• Various Improvements

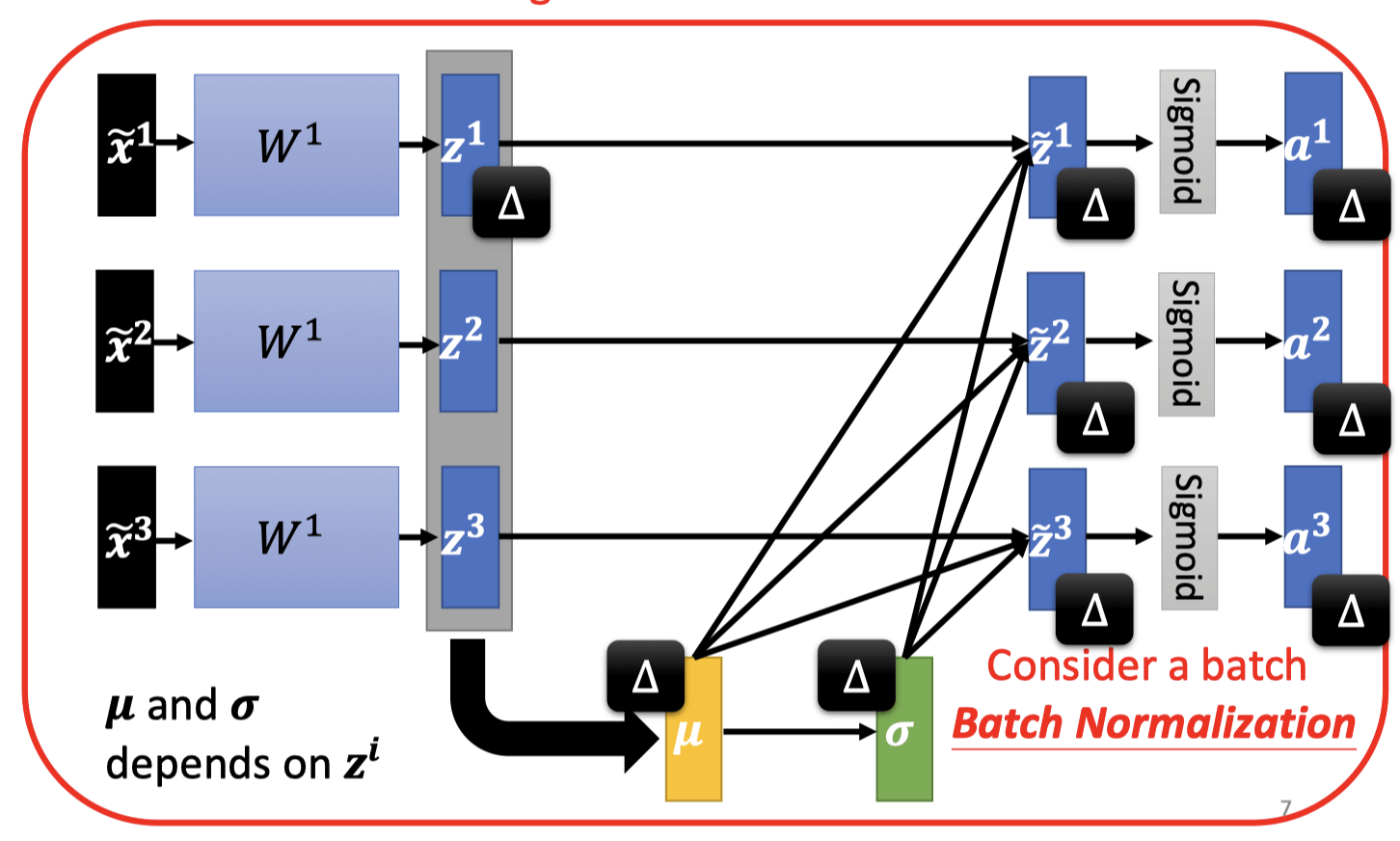
Batch Normalization

把error surface的山铲平

假设一个简单的网络

$$y = w_1x_1+w_2x_2+b$$

当$x_1$很小，$x_2$很大时，$w_1$的变化对Loss的影响很小，$w_2$的变化对Loss的影响很大，就会出现图中左边的情况。

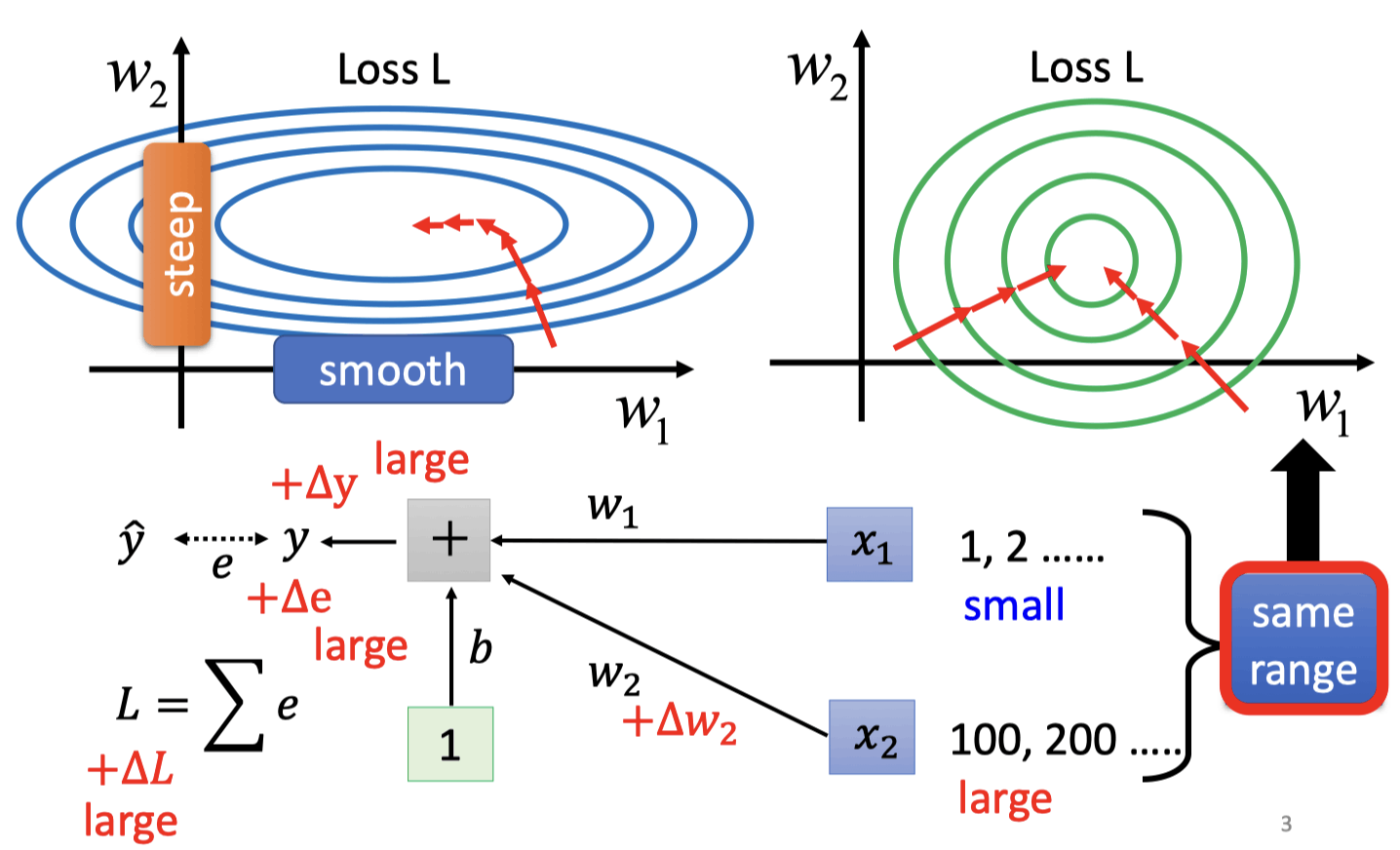
让输入feature不同的dimension有相同的数值范围，得到更好的error surface

Feature Normalization

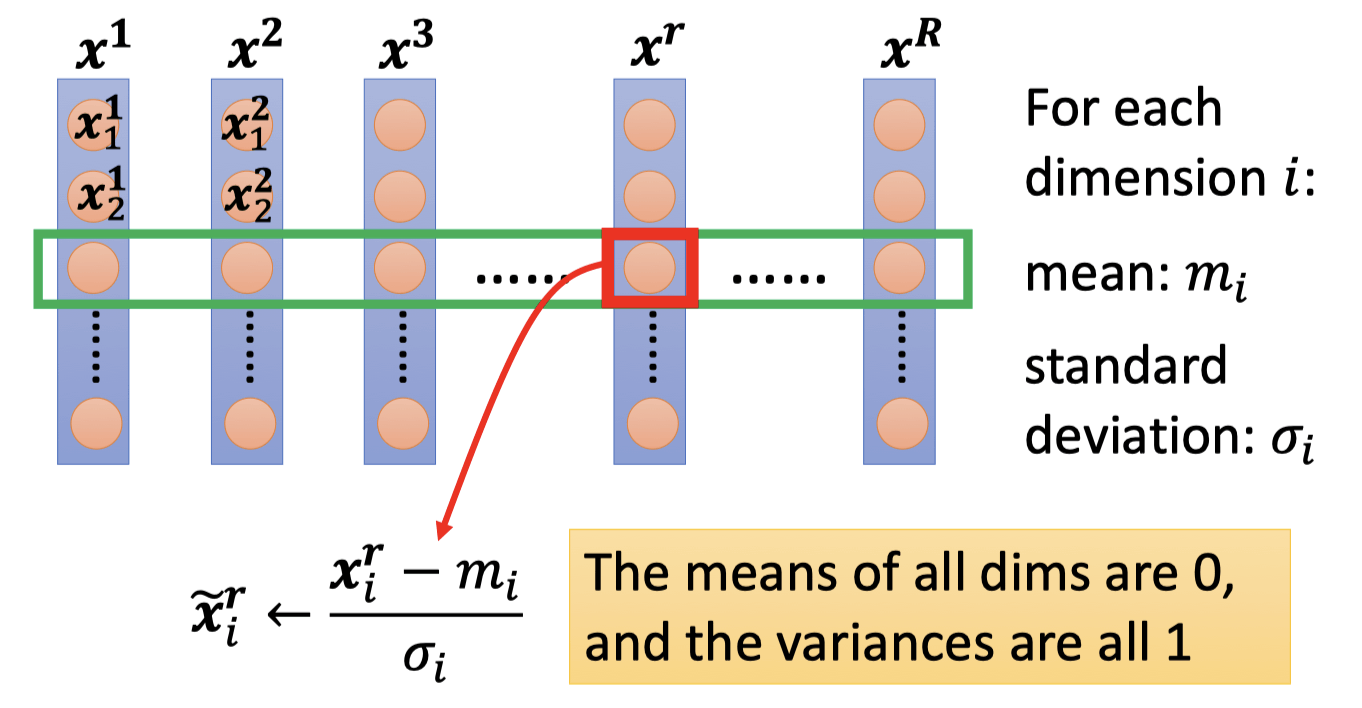
In general, feature normalization makes gradient descent converge faster.

• Considering Deep Learning

This is a large network! 每一个batch是一个更大的网络

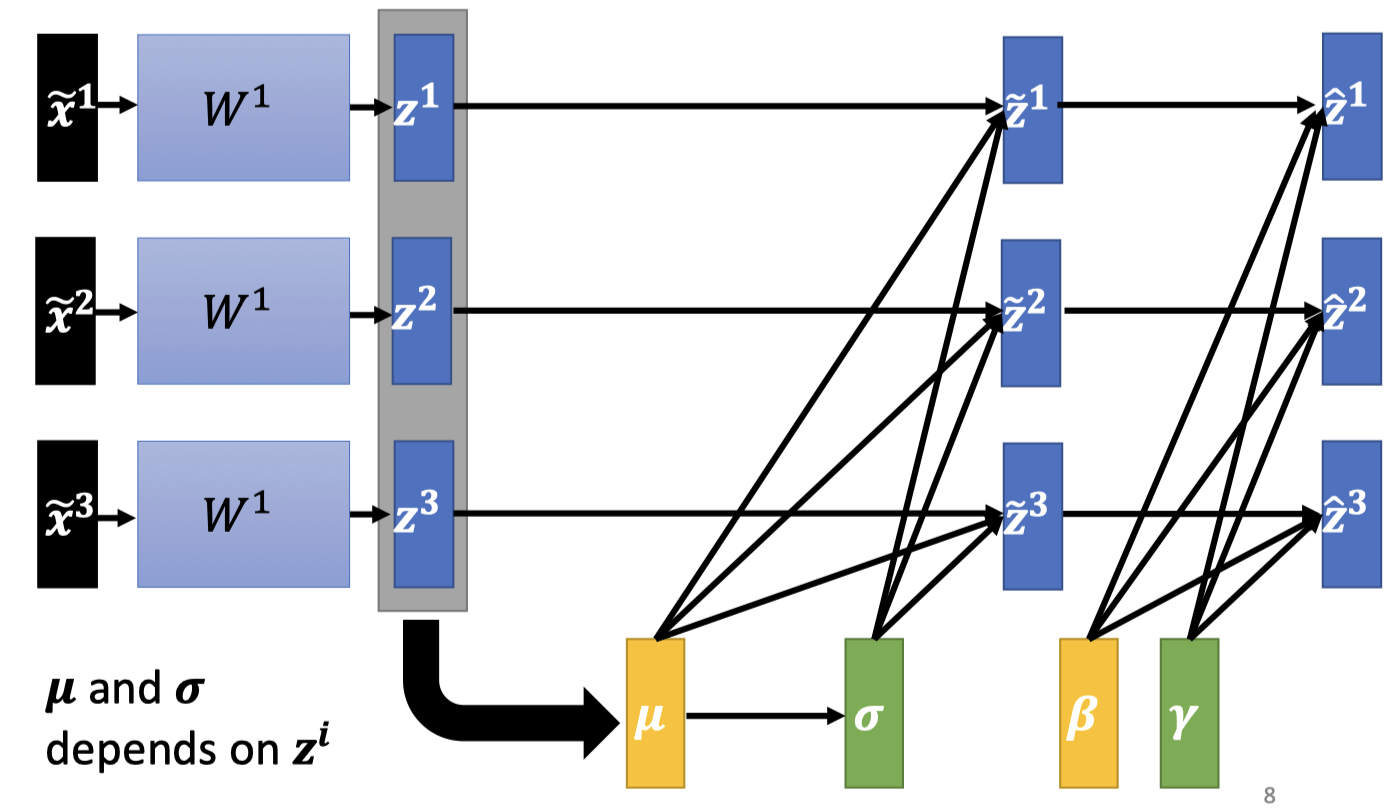
Normalization后在乘以$\gamma$再加$\beta$，$\gamma$和$\beta$是网络内可学习的参数。

因为Normalization后$\widetilde{z}^{i}$的均值为0，这个限制可能会对网络产生不好的影响，$\gamma$再加$\beta$让网络输出的均值不一定是0

$\gamma$初始化为1 vector，$\beta$初始化为0 vector

$$\widetilde{z}^{i}=\frac{z^i-\mu}{\sigma} \\ {\hat{z} }^{i}=\gamma\Theta{\widetilde{z} }^{i}+\beta$$

Testing

We do not always have batch at testing stage.

Computing the moving average of $\mu$ and $\sigma$ of the batches during training.

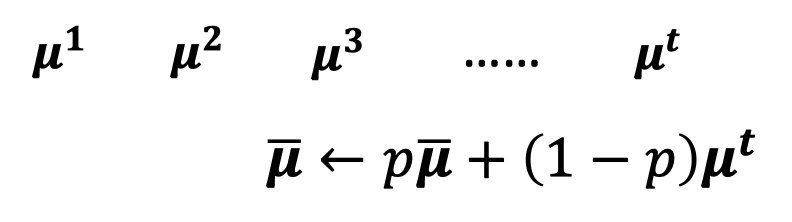
BN on CNN

在卷积层后面的BN与1d情况的BN层是很类似的，同样是沿着batch的维度求均值和方差。并且，它的参数大小也仅仅与feature dim（channels）有关，也为2*d。 但是，有一点需要注意的是，在求均值和方差的时候，实际上其不仅是沿着batch的维度求取，在每个channel上的宽度和高度方向也求取均值。

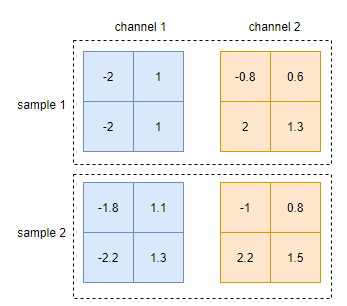
均值和方差的shape是[1, 2, 1, 1]。也就是说，求取均值和方差时，是沿着batch, h, w三个维度进行的，只保证每个channel的统计值是独立的，所以求得均值和方差：

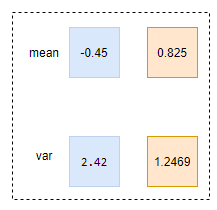
To learn more

• Batch Renormalization: https://arxiv.org/abs/1702.03275

• Layer Normalization: https://arxiv.org/abs/1607.06450

• Instance Normalization: https://arxiv.org/abs/1607.08022

• Group Normalization: https://arxiv.org/abs/1803.08494

• Weight Normalization: https://arxiv.org/abs/1602.07868

• Spectrum Normalization: https://arxiv.org/abs/1705.10941

参考

1. https://speech.ee.ntu.edu.tw/~hylee/ml/2021-spring.php
2. https://www.bilibili.com/video/BV1Wv411h7kN
3. https://zhuanlan.zhihu.com/p/403073810